I 권
공리
공리 1
임의의 서로 다른 두 점을 잇는 선분을 유일하게 그을 수 있다.
애플릿
부연설명
현대적익 용어로 이 명제를 다음과 같이 서술한다.
'임의의 점 \(\rm A\)에서 다른 임의의 점 \(\rm B\)로 선분 \(\rm AB\)를 유일하게 그을 수 있다.'
이 명제는 눈금없는 곧은자로 선분을 그을 수 있는 것을 말한다. 유클리드는 유일하다는 단어는 사용하지 않고 암묵적으로 이를 인정하였다.
이 공리는 정의와 결합하여 알 수 있는 것이 있다. 즉, 두 선분의 양 끝점이 같으면 그들은 전체 모든 곳에서 서로 일치한다. 이와 동등한 공리인 "두 선분은 어떤 넓이를 둘러쌀 수 없다."는 공리가 흔히 기하학 원에 덧붙여 나온다.
생각해 보기
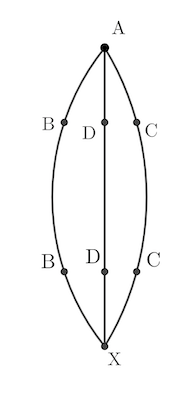
두 선분이 어떤 영역을 둘러싸고 이들 양 끝 점이 \(\rm A\), \(\rm X\)라고 하면, 선분의 양 끝점을 고정시킨 채 회전시키면 모든 점들은 계속해서 제자리에 남아 있어야 하며, 회전한다고 해도 다른 위치로 이동 되지 않기 때문에 이들 둘 다 또는 둘 중 어느 하나는 직선이 아니다.