I 권
공리
공리 5
주어진 2 개의 직선이 있고, 다른 한 직선이 이 2 개의 직선과 만나는데, 어느 한쪽의 두 내각을 더한 것이 보다 작다고 하자. 그러면, 2개의 직선을 길게 늘였을 때, 두 직선의 내각을 더한 것이 보다 작은 쪽에서 만난다.
주어진 직선과 그 직선 위에 있지 않은 점을 지나면서 주어진 직선에 평행한 직선을 오직 한 개 만을 그릴 수 있다.
애플릿
부연설명
이 공리에서는 두 개의 직선을 다른 한 직선이 지난다. 그러면 그에 의해서 생기는 동측 내각의 합이 \(2 \angle \rm{R}\)보다 작은 쪽에서 교점이 생긴다는 의미이다.
그림에서 각 \(\rm ABE\)와 각 \(\rm BED\) 가 두 직각(180°)보다 작으면 선분 \(\rm AC\)와 \(\rm DF\)가 점 \(\rm A\)와 점 \(\rm D\)의 방향으로 확장될 때 만난다. 이 공리는 평행선의 속성을 증명하는 데 사용할 수 있기 때문에 일반적으로 "평행선 공리"라고 한다.
현제는 유클리드 5번째 공리와 동치 명제인 “직선 \(l\)위에 있지 않은 점 \(\rm{P}\)을 지나면서 직선 \(l\) 에 평행한 직선 \(m\)을 유일하게 한 개를 작도 할 수 있다.”을 사용하고 있다.
생각해 보기
평행선 공리는 역사적으로 가장 흥미로운 공리이다. 여러 시대에 걸쳐 기하학자들은 평행선 공리가 필요가 없도록 나머지 공리들로부터 증명하려고 수 많은 시도를 하였다. 이러한 시도는 그 거짓된 공리를 가정한 다음 모순을 도출하는 것이었다. 많은 기이한 결론이 평행선 공리를 부정함으로써 따르며, 몇몇 기하학자들은 평행선 공리가 나머지로부터 따랐다고 결론지을 정도로 큰 부조리를 발견하였다.
그럼에도 불구하고 이러한 명백한 부조리는 모순이 아니다. 19세기 초 볼리야(Bolyai), 로바체스키(Lobachevsky), 가우스(Gauss)는 이러한 비유클리드 기하학을 다루는 방법을 찾았고, 비록 유클리드 기하학과는 매우 다르지만 유효한 기하학으로 받아들였다. 이 쌍곡선 기하학은 유클리드 기하학과 마찬가지로 일관성이 있으며 많은 활용도가 있다.
프앙카레(Poincaré)는 쌍곡선 평면의 "점"이 고정된 원 내부의 점으로 간주되는 쌍곡선 기하학의 유용한 모델을 설명하였다. 쌍곡기하학은 원에서 호를 직선이라고 하면 직선 밖의 점을 지나고 주어진 직선에 평행한 즉, 교점을 갖지 않는 수 많은 직선이 존재한다.
타원기하학은 구에서 대원을 직선이라고 하면 직선 밖의 점을 지나고 주어진 직선에 평핸한 직선은 없다. 즉, 두 직선은 모두 교점을 갖는다.
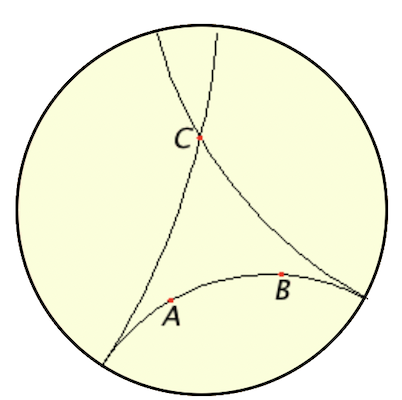
쌍곡기하학에서의 삼각형의 내각의 합은 \(180^\circ\)보다 작고,(위 그림 참조)
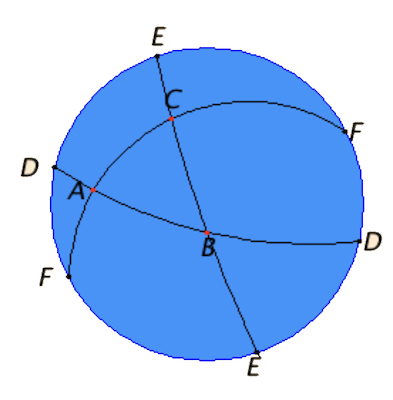
타원기하학에서의 삼각형의 내각의 합은 \(180^\circ\)보다 크다.(위 그림 참조)