I 권
공리
공리 4
모든 직각은 서로 같다.
애플릿
부연설명
점 \(\rm D\)에서 선분 \(\rm AB\)로의 수선의 발을 \(\rm C\)라고 하자. 그러면 각 \(\rm ACD\)와 \(\rm BCD\)가 \(\angle\rm ACD=\angle\rm BCD=90^\circ\)이라는 것은 분명하다. 그래서 이 공리는 각 \(\rm ACD\)와 점 \(\rm H\)에서 선분 \(\rm EF\)에 내린 수선의 발을 \(\rm G\)라 할 때 생기는 다른 직각인 각 \(\rm EGH\)는 \(\angle\rm ACD=\angle\rm EGH=90^\circ\)이라는 것을 의미한다.
이 공리는 각의 크기를 측정하는데 사용된다. '원론'에서 유일하게 측정된 각의 크기는 직각(\(90^\circ\)) 뿐이다. 또한 도형이 이동할 때 변하지 않는다는 공리가 필요하기도 하다.
생각해 보기
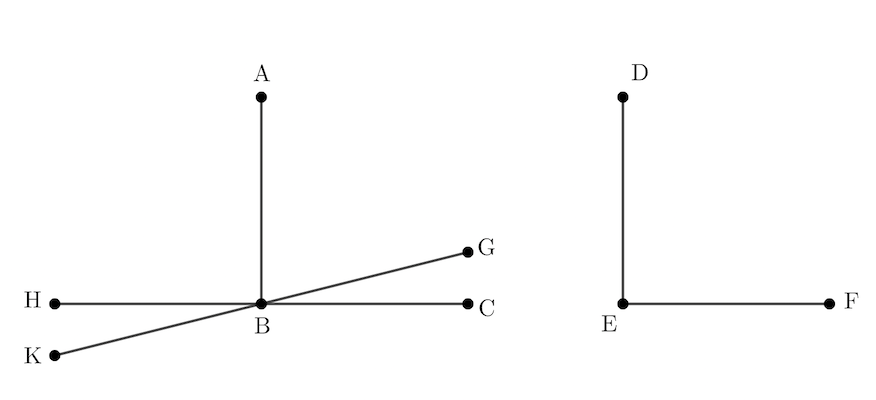
[그림]과 같이 \(\rm\angle ABC=\angle DEF=90^\circ\)이라고 하자.
만약 \(\rm\angle ABC \ne \angle DEF=90^\circ\)이라고 하면 두 각 중 어느 하나가 더 클것이다.
예를 들어, \(\rm\angle ABC > \angle DEF\)이라고 하자.
그러면 선분 \(\rm DE\)를 선분 \(\rm AB\)에 포개어 지도록 각 \(\rm DEF\)를 평행이동하자. 그러면 선분 \(\rm EF\)는 각 \(\rm ABC\) 안에 놓이게 된다. 즉, \(\rm BG\) 처럼 놓인다.
선분 \(\rm CB\)를 길게 늘여서 선분 \(\rm HC\)를 그리자. 그러면 \(\rm\angle ABC=90^\circ\)이므로 \(\rm\angle ABH=90^\circ\)이다. 따라서 \(\rm\angle ABC=\angle ABH\)이다. 그리고 직각의 정의에 의해서 서로 이웃한 각이 서로 같다. 그러므로 \(\rm\angle ABH > \angle ABG \)이다. --- (1)
선분 \(\rm GB\)를 길게 늘여서 선분 \(\rm GK\)를 그리자. 그러면 같은 이유로 \(\rm\angle ABK=\angle ABG=90^\circ\)이므로 \(\rm\angle ABH < \angle ABG\)이다. --- (2)
그런데 (1)과 (2)에 의해서 \(\rm \angle ABG < \angle ABH < \angle ABG\)이다.
이것은 모순이다.
그러나 프로클루스의 이러한 증명도 두 선분 \(\rm CB\), \(\rm GB\)를 늘일 수 있는 방법이 한가지라서, 선분 \(\rm BK\)가 각 \(\rm ABH\)의 바깥쪽에 놓인다는 가정이 필요하다. 이 가정을 또 증명해햐 한다.