I 권
명제
명제 2 (문제)
주어진 한 점과 유한한 길이의 선분에 대하여, 한 끝 점이 주어진 점이고 길이가 주어진 선분의 길이와 같은 선분을 그리시오.
주어진 점\(\rm A\)와 선분 \(\rm BC\)에 대하여, 점 \(\rm A\)를 한 끝 점으로 하고 길이가 \(\overline{\rm BC}\)인 선분을 그리시오.
애플릿
증명
주어진 점 \(\rm A\)와 선분 \(\rm BC\)에 대하여 점 \(\rm A\)를 한 끝점으로 하고 길이가 \(\overline{\rm BC}\)인 선분을 그려야 한다.
1) 풀이(작도)
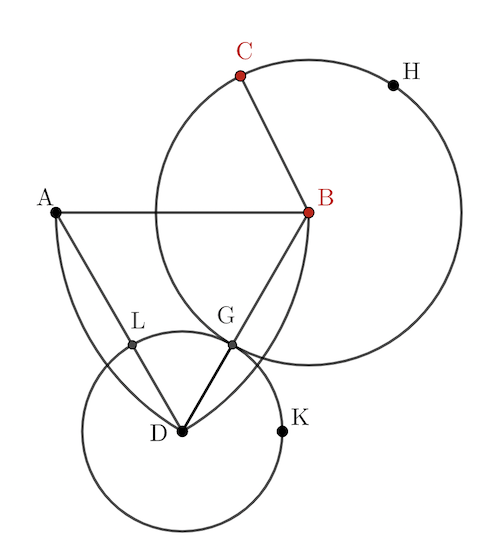
점 \(\rm A\)에서 점 \(\rm B\)로 선분 \(\rm AB\)를 그리자. [I권 공리1]
선분 \(\rm AB\)가 한 변인 정삼각형 \(\rm DAB\)를 작도 하자. [I권 명제 1]
그러면 \(\overline{\rm DA}=\overline{\rm DB}=\overline{\rm AB}\)이다.
두 선분 \(\rm DA\), \(\rm DB\)를 연장하여 각각 선분 \(\rm DE\), \(\rm DF\)를 그리자. [I권 공리2]
중심이 \(\rm B\)이고 반지름이 \(\overline{\rm BC}\)인 원 \(\rm GCH\)를 그리자. [I권 공리3]
원 \(\rm GCH\)와 선분 \(\rm DF\)와의 교점을 \(\rm G\)라고 하자.
또한 중심이 \(\rm D\)이고 반지름이 \(\overline{\rm DG}\)인 원 \(\rm GKL\)를 그리자. [I권 공리3]
원 \(\rm GKL\)와 선분 \(\rm DE\)와의 교점을 점 \(\rm L\)라고 하자.
2) 증명(논리적 정당화)
점 \(\rm B\)는 원 \(\rm CGH\)의 중심이고, 두 점 \(\rm C\), \(\rm G\) 모두 원 \(\rm CGH\) 위의 점이므로 \(\overline{\rm BC}=\overline{\rm BG}\)이다.
또한 점 \(\rm D\)는 원 \(\rm GKL\)의 중심이고 두 점 \(\rm L\), \(\rm G\)는 원 \(\rm GKL\) 위의 점이므로 \(\overline{\rm DL}=\overline{\rm DG}\)이다.
따라서 \(\overline{\rm DB}+\overline{\rm BG}=\overline{\rm DA}+\overline{\rm AL}\)이다. [I권 정의 15] --- ①
따라서 삼각형 \(\rm DAB\)가 정삼각형이어서 \(\overline{\rm DB}=\overline{\rm DA}\)이다. --- ②
식 ①에서 식 ②를 변변끼리 각각 빼면 \(\overline{\rm AL}=\overline{\rm BG}\)이고 [I권 일반상식 3]
어떤 것 둘이 어떤 것과 서로 같다면, 그 둘도 서로 같으므로 \(\overline{\rm BC}=\overline{\rm BG}=\overline{\rm AL}\)이다. [I권 일반상식 1]
그러므로 선분 \(\rm AL\)은 한 끝 점이 \(\rm A\)이고 \(\overline{\rm AL}=\overline{\rm BC}\)인 선분이다.
Q.E.F.
작도 애플릿
정당화 애플릿
부연설명
애플릿
작도만을 생각해서는 정삼각형 \(\rm ABC\)를 작도를 할 필요성은 없다.
중심이 점 \(\rm A\)이고 반지름이 \(\overline{\rm AB}\)인 원과 중심이 점 \(\rm B\)이고 반지름이 \(\overline{\rm AB}\)인 원의 두 교점 중 한 점을 점 \(\rm D\)이라고 하자.
그리고 중심이 점 \(\rm B\)이고 반지름이 \(\overline{\rm BC}\)인 원을 작도하고 이 원과 반직선 \(\rm DB\)와의 교점을 점 \(\rm G\)라고 하자.
또한 중심이 점 \(\rm D\)이고 반지름이 \(\overline{\rm DG}\)인 원과 반직선 \(\rm DA\)의 교점을 점 \(\rm L\)이라고 하자.
\(\overline{\rm DL}=\overline{\rm DG}\)
\(\overline{\rm DA}+\overline{\rm AL}=\overline{\rm DB}+\overline{\rm BG}\)
이고 \(\overline{\rm AB}=\overline{\rm DA}=\overline{\rm DA}\)이므로 \(\overline{\rm AL}=\overline{\rm BG}\)이다.
또한 \(\overline{\rm BG}=\overline{\rm BC}\)이므로 \(\overline{\rm AL}=\overline{\rm BG}=\overline{\rm BC}\)이다.
따라서 \(\overline{\rm AL}=\overline{\rm BC}\)이다.
Q.E.D.
생각해 보기
이것은 자명하다. \(\overline{\rm AB}=\overline{\rm BC}\)인 경우 이미 점 \(\rm A\)에서 \(\overline{\rm AB}=\overline{\rm BC}\)인 선분 \(\rm AB\)를 이미 그렸다.
점 \(\rm G\)의 위치가 선분 \(\rm BD\) 반직선 \(\rm BD\)의 점 \(\rm D\) 바깥쪽에 놓여 있는 경우이다.
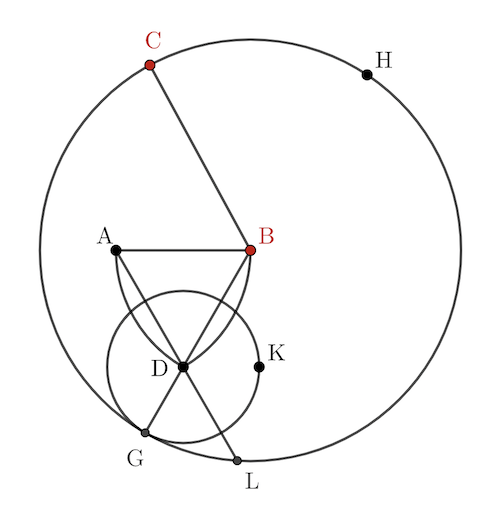
점 \(\rm G\)의 위치가 선분 \(\rm BD\) 위에 놓여있어 정삼각형 \(\rm ABD\)의 변들을 늘릴 필요가 없는 경우이다.